Nowcasting GDP with PMI using MIDAS-GETS
The latest from the EViews blog:
Nowcasting, the act of predicting the current or near-future state of a macro-economic variable, has become one of the more popular research topics performed in EViews over the past decade.
Perhaps the most important technique in nowcasting is mixed data sampling, or MIDAS. We have discussed MIDAS estimation in EViews in a couple of prior guest blog posts, but with the introduction of a new MIDAS technique in the recently released EViews 12, we thought we'd give another demonstration.
Table of Contents
MIDAS – A Brief Background
Mixed Data Sampling (MIDAS) is a regression technique that handles the case where the dependent variable is sampled or reported at a lower frequency than that of one, or more, of the independent regressors. This is common in macroeconomics where a number of important indicators, such as GDP, are usually reported on a quarterly basis, and other indicators, such as unemployment or stock prices, are reported on a monthly or even weekly basis.
The traditional approach to dealing with this mixed-frequency problem is to aggregate the higher-frequency variable into the same frequency as the lower. For example, when dealing with quarterly GDP and monthly unemployment, it's common practice to use the average monthly unemployment rate over the three months in a quarter as a single quarterly observation. Whilst simple to implement, this approach loses fidelity in the higher-frequency variables. Any within-quarter movements in unemployment are lost, and the dataset is reduced by 2/3 (converting three observations into one).
MIDAS alleviates this issue by adding the individual components of the higher-frequency variable as independent regressors, allowing a separate coefficient for each component. For example, unemployment could have three separate regressors, one for the first month of the quarter, one for the second, and one for the third. This simple approach is called U-MIDAS.
A drawback of creating a regressor for each high-frequency component is that, in certain cases, one quickly saturates the equation with many regressors (curse of dimensionality). For instance, whereas monthly unemployment and quarterly GDP would generate 3 regressors for the one underlying variable, annual data would generate 12 regressors. If we had daily interest rates regressed with quarterly data, we would have over 90 regressors for the one underlying variable.
To mitigate this expansion of regressors, traditional MIDAS utilizes a selection of weighting schemes that parameterize the higher frequency variables into a smaller number of coefficients. The most common of these weighting schemes is Almon/PDL weighting.
A last note on MIDAS – although it is natural to want to include a number of high-frequency variables equal to the number of high-frequency periods per low frequency period (i.e. include three monthly variables since there are three months in a quarter), there is nothing that mathematically imposes this restriction in the MIDAS framework, and it is quite common to use many more variables than the natural number.
Going back to our unemployment/GDP example, you may want to utilize 9 months of unemployment data to explain GDP, and thus create 9 variables. In other words, you may determine that Q1 GDP is determined by unemployment in March, February, January (the three natural months), as well as 6 months previous (December, November, October, September, August, July).
Of course, you can also impose a lag structure to postulate that Q1 GDP is determined by February, January, …., June (a one month lag), or is determined by December, November, …, April (a three month lag). These 9 variables may then be reduced to a smaller number of coefficients using MIDAS weighting schemes, or, if the sample size permits, kept at 9 separate regressors.
MIDAS-GETS
EViews 12 introduces a new MIDAS estimation method, MIDAS-GETS. Rather than using a weighting scheme to reduce the number of variables, MIDAS-GETS controls the curse of dimensionality with the Auto-Search/GETS variable selection algorithm to select which of the high frequency variables to include in the regression.
Since the Auto-Search/GETS algorithm is also used in EViews' indicator saturation detection routines, indicator saturation is available to MIDAS-GETS too. This means that the estimation can automatically include indicator variables that allow for outliers and structural changes in the model, which can dramatically enhance the forecasting performance of a model.
MIDAS as a Nowcasting Tool
Although MIDAS was not necessarily introduced as a tool for nowcasting, its applicability to nowcasting is obvious; whilst traditional macroeconomic variables are typically sampled at low frequencies and with a reporting delay, high frequency data is available in a timely fashion that can often be used to estimate the current state of a low frequency variable.
More concretely, take Eurozone GDP. This important macro variable is released by Eurostat on a quarterly basis, usually 3 months after the quarter has ended. Thus, if you are at the end of July and want to know what the current GDP is, you must wait until December to receive the official statistics.
However, there may be monthly, or even daily variables, available without a delay. Unlike their latent counterparts, these can be used to estimate the current value of GDP immediately.
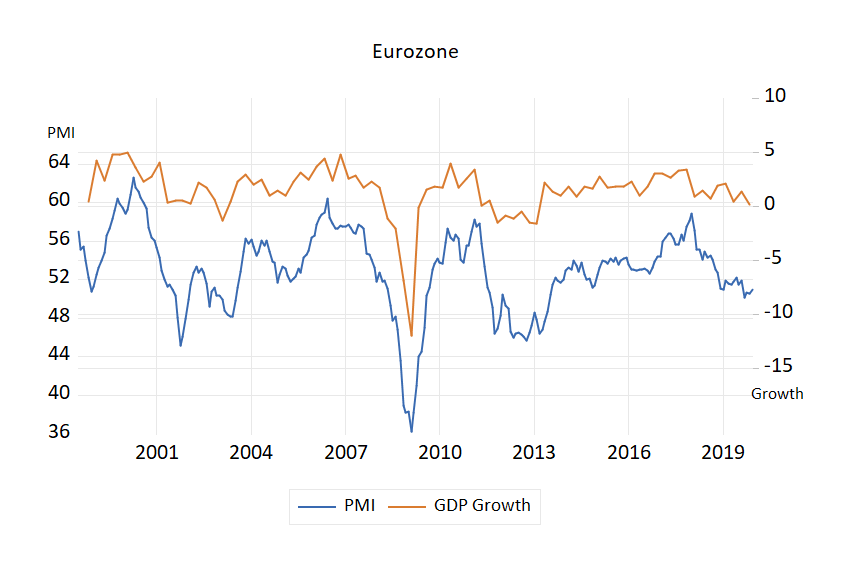
PMI as a Nowcasting Instrument
One of the more popular variables used in nowcasting exercises are economic surveys. Surveys can be released at a high frequency with little delay and are often highly correlated with more traditional macroeconomic variables. Here at EViews we're fans of the Purchasing Manager's Index (PMI). The latter is derived from surveys of senior executives at private sector companies, is released monthly, and reflects the current state of the economy (i.e., has little delay between the survey and the release). In particular, we like the Eurozone composite measure which consistently shows a high correlation with growth in Eurozone GDP:
 |
Nowcasting Exercises
As a simple demonstration of nowcasting with various MIDAS approaches, we're going to run a little exercise that uses monthly Eurozone composite PMI to nowcast quarterly Eurozone GDP growth.
Specifically, we have an EViews workfile with two pages: the first contains quarterly data from 1998q3 to 2020q3 with Eurozone GDP Growth (GDP_GR), whereas the second contains monthly data over the same period with Eurozone Composite PMI (PMICMPEMU).
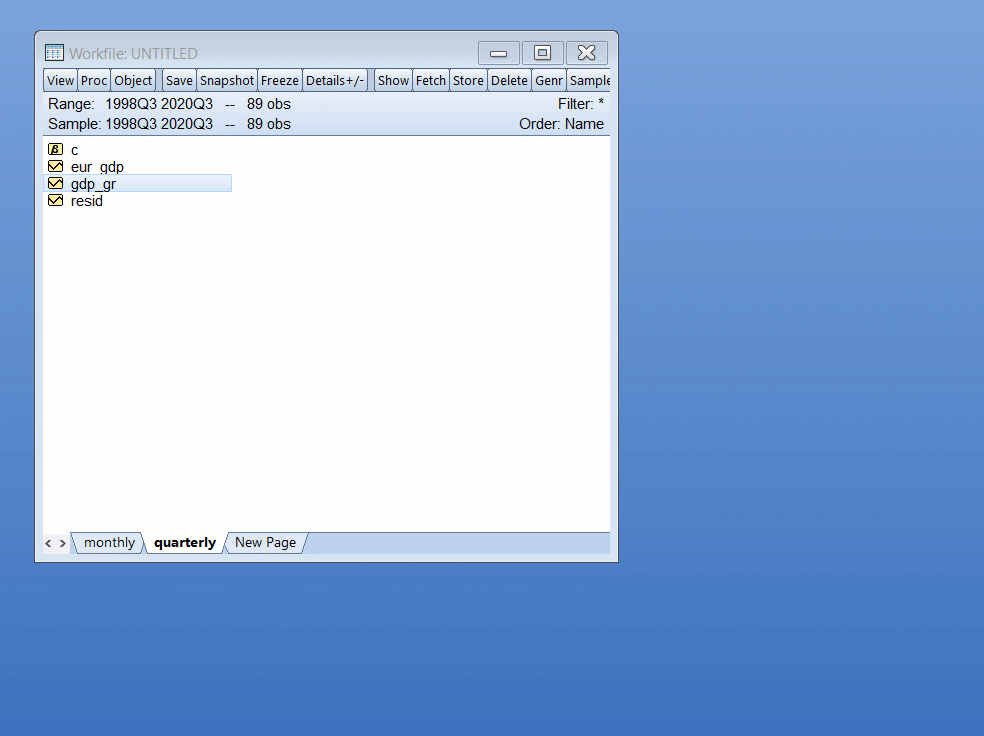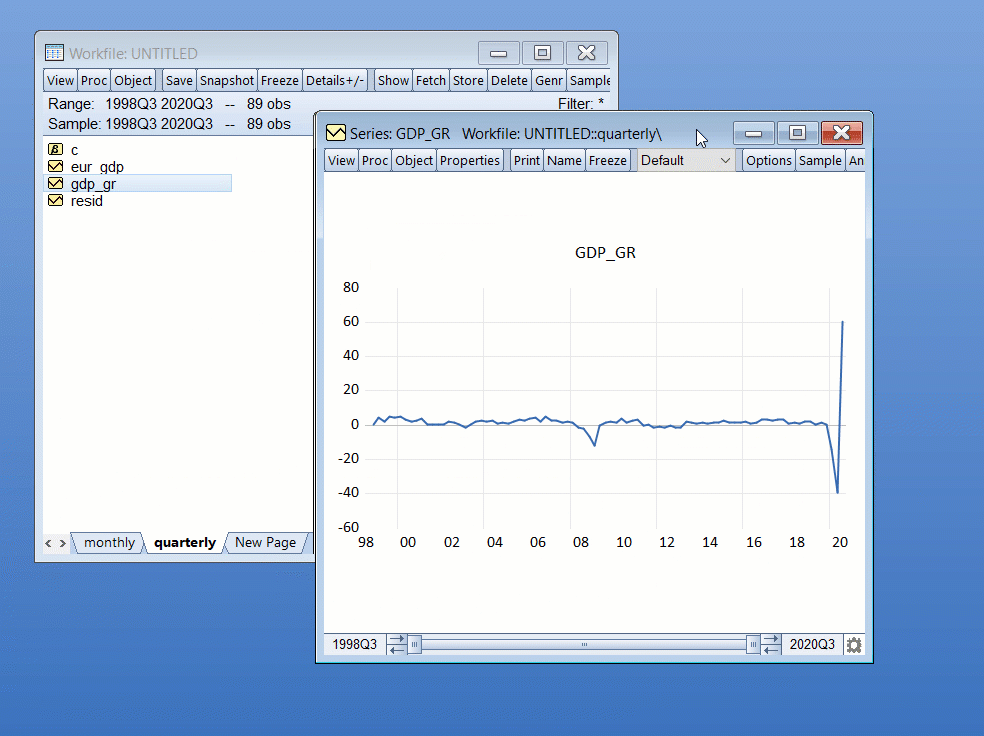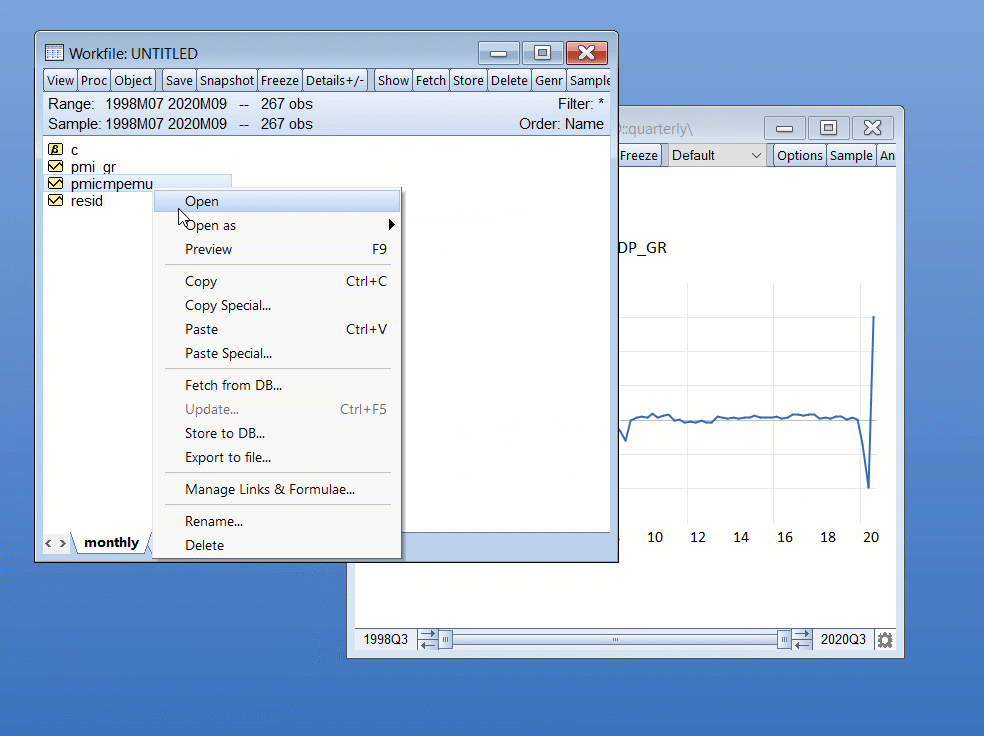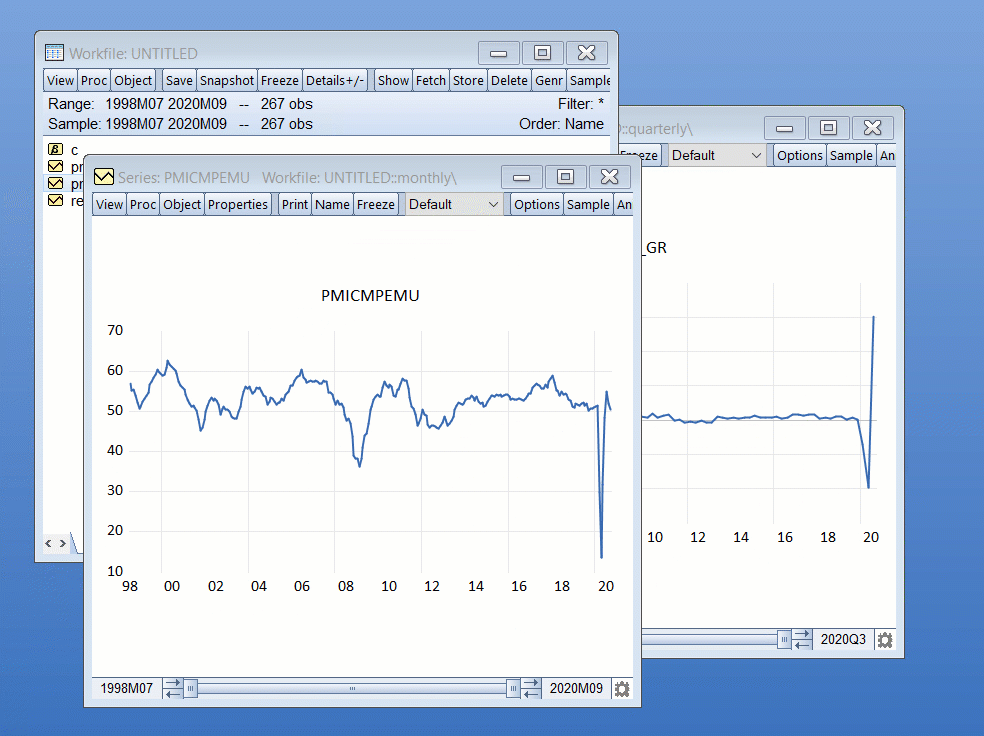 |
MIDAS-PDL
To begin, we'll pretend we are currently at the start of March 2019 and wish to nowcast the current (2019Q1) value of Eurozone GDP growth. We have our February PMI data handy (and all previous months). We'll estimate a standard MIDAS equation in EViews, using data until Q4 2018 to estimate our model, then use the February PMI with that equation to nowcast Q1 2019. We'll assume that GDP growth is explained by 12 months of PMI data and by the previous quarterly value of GDP growth. The steps we perform are:
- Ensure we have the Quarterly page selected.
- Quick->Estimate Equation
- Select MIDAS as the Method.
- Enter GDP_GR C GDP_GR(-1) as the dependent variable and quarterly regressors (a constant and the lagged value of GDP growth).
- Enter Monthly\PMICMPEMU(-1) as the high frequency regressor. The (-1) here indicates that we wish to use data up until the second month of the quarter (the default is the third/last month of the quarter, so by lagging it one month, we use data until the second month).
- Set the Sample to end in 2018q4.
 |
The default MIDAS weighting method in EViews is PDL/Almon weighting with a polynomial degree of 3, which is what we'll use if we just click OK:
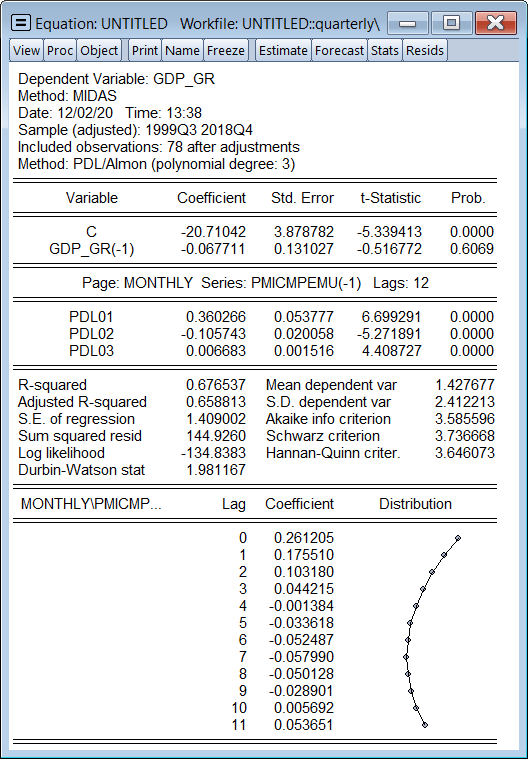 |
Since this is a forecasting/nowcasting exercise, we won't delve into interpretation of these results, other than to note that all three MIDAS PDL terms are statistically significant.
Now, to perform the nowcast, we can simply use EViews' built in forecast engine and forecast for the “current” quarter (2019Q1). This is done with the following steps:
- Click the Forecast button to bring up the forecast dialog.
- Change the Forecast sample to 2019Q1 2019Q1 (just a single period).
- Click OK.
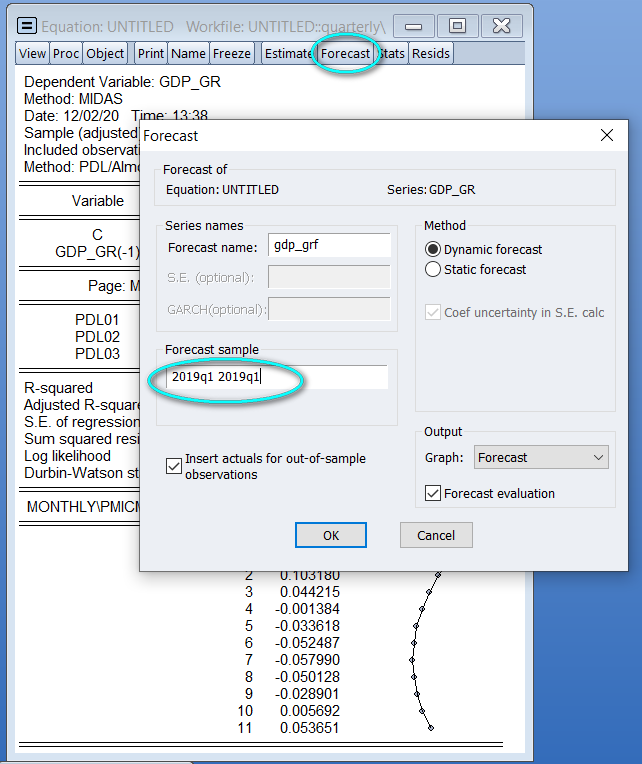 |
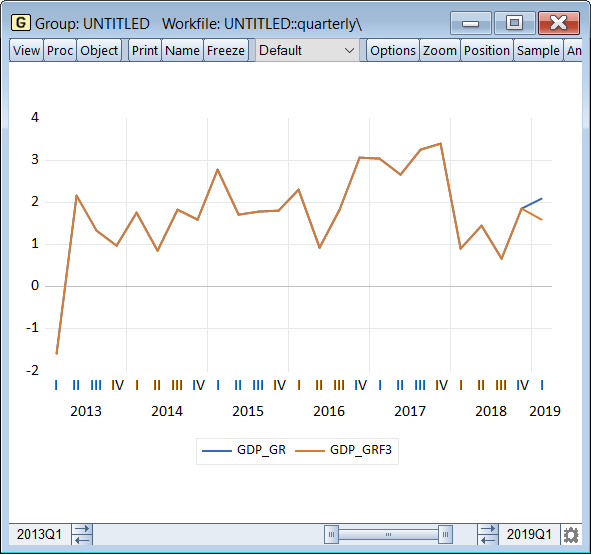
The forecast will produce a new series in the workfile, GDP_GRF containing actual values for all observations other than 2019Q1, where it will contain the forecasted value. We can open this series together with the actual series in a group, and then graph it to see how close the single forecasted value is to the historical actual:
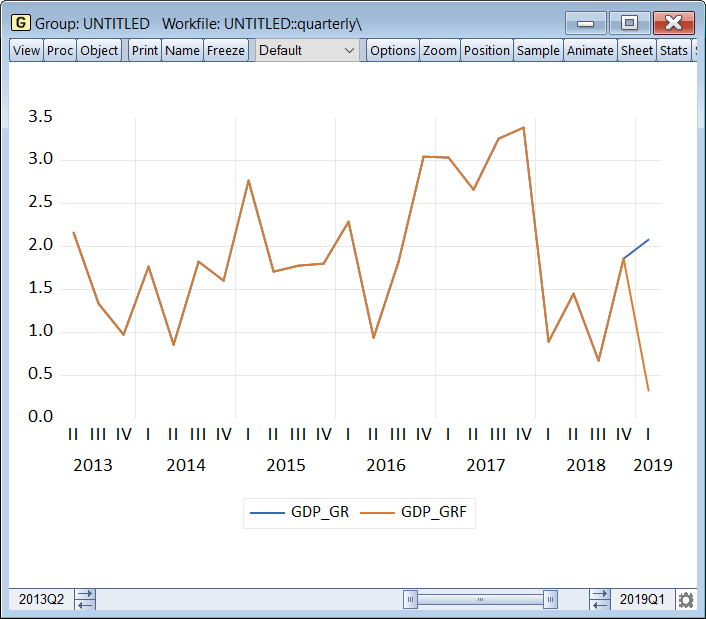 |
The results seem a little underwhelming despite being just a single observation. Let's see if we can improve this forecast with the new MIDAS-GETS weighting method.
MIDAS-GETS
To perform the new estimation, we undertake the same steps as before, but additionally change the weighting method:
- Quick->Estimate Equation
- Select MIDAS as the Method.
- Enter GDP_GR C GDP_GR(-1) as the dependent variable and quarterly regressors.
- Enter Monthly\PMICMPEMU(-1) as the high frequency regressor.
- Enter 12 as the Fixed Lags parameter to indicate each quarter is explained by 12 months of data.
- Set the Sample to end in 2018q4.
- Switch the Options Tab.
- Change MIDAS weights to Auto/GETS.
 |
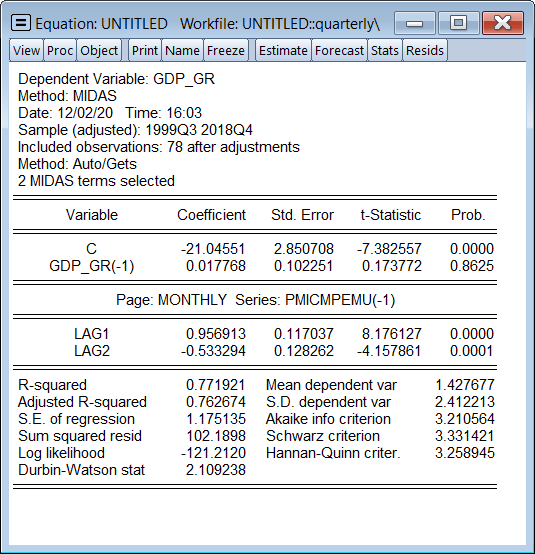 |
Again, we won't delve into interpretation of these results, other than to mention that out of the 12 months of possible PMI data that could be used to explain each quarter, the equation chose to use only the two most recent months (denoted lags). We'll follow the exact same steps as previously to produce a forecast from this equation:
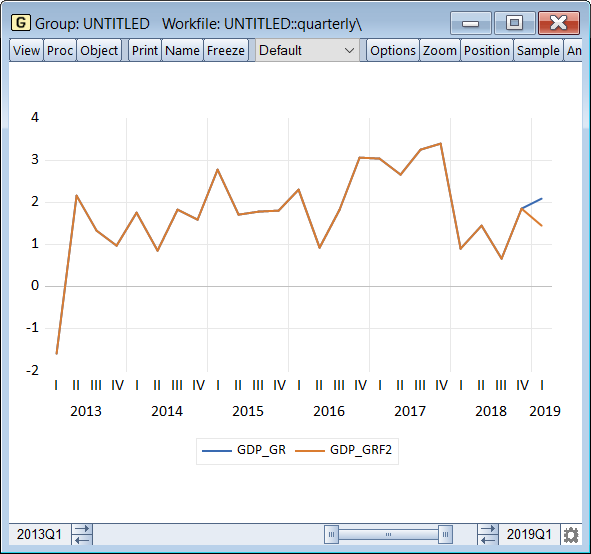 |
The nowcast looks better than the previous model's, although again it is only a single data point.
MIDAS-GETS with Indicator Saturation
Finally, we'll estimate a MIDAS-GETS model that includes indicator saturation. This will automatically model outliers and structural changes in our equation. We follow the same steps as before but use the Auto/GETS options button to include searching for indicator variables. We will, in this case, search for outliers by only selecting impulse indicators.
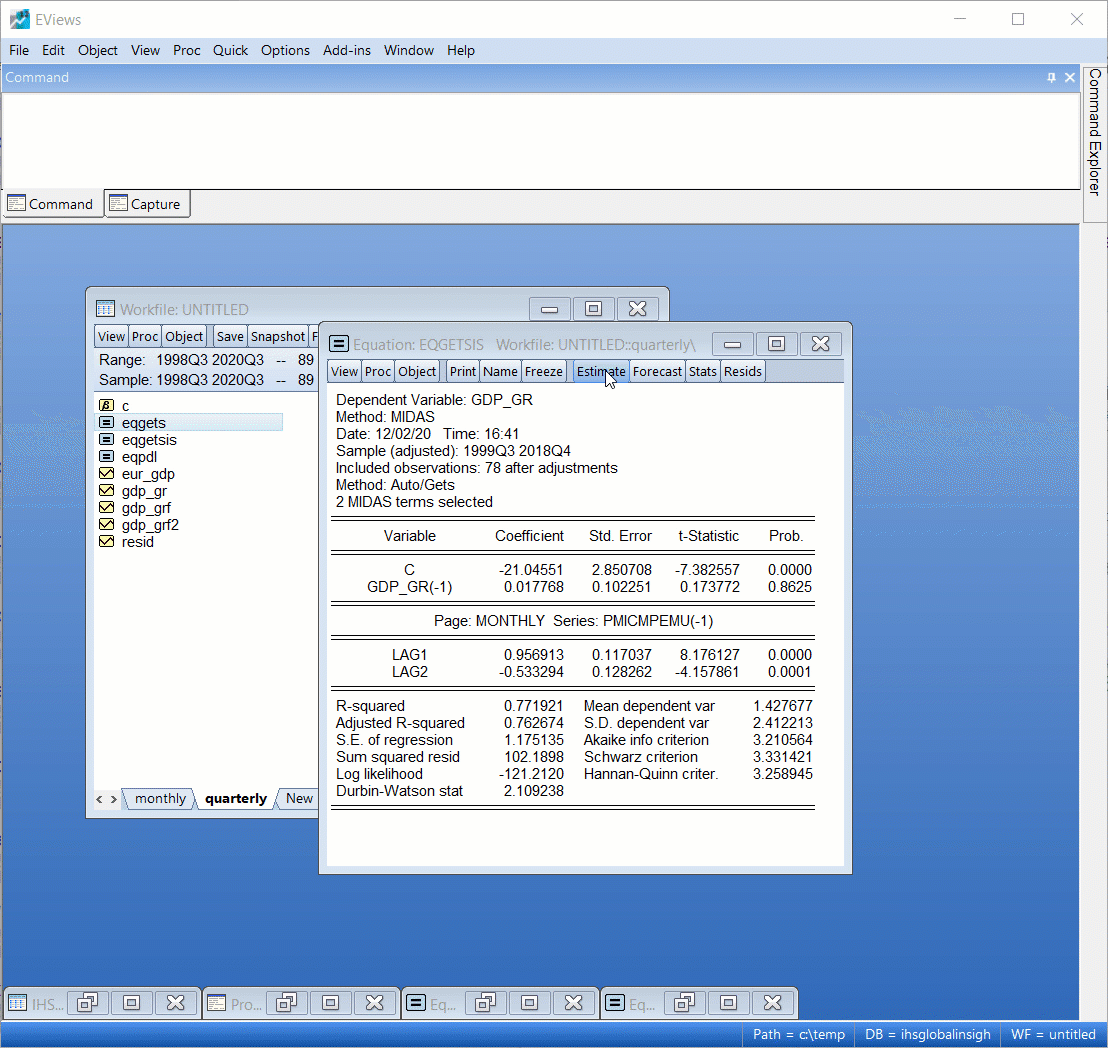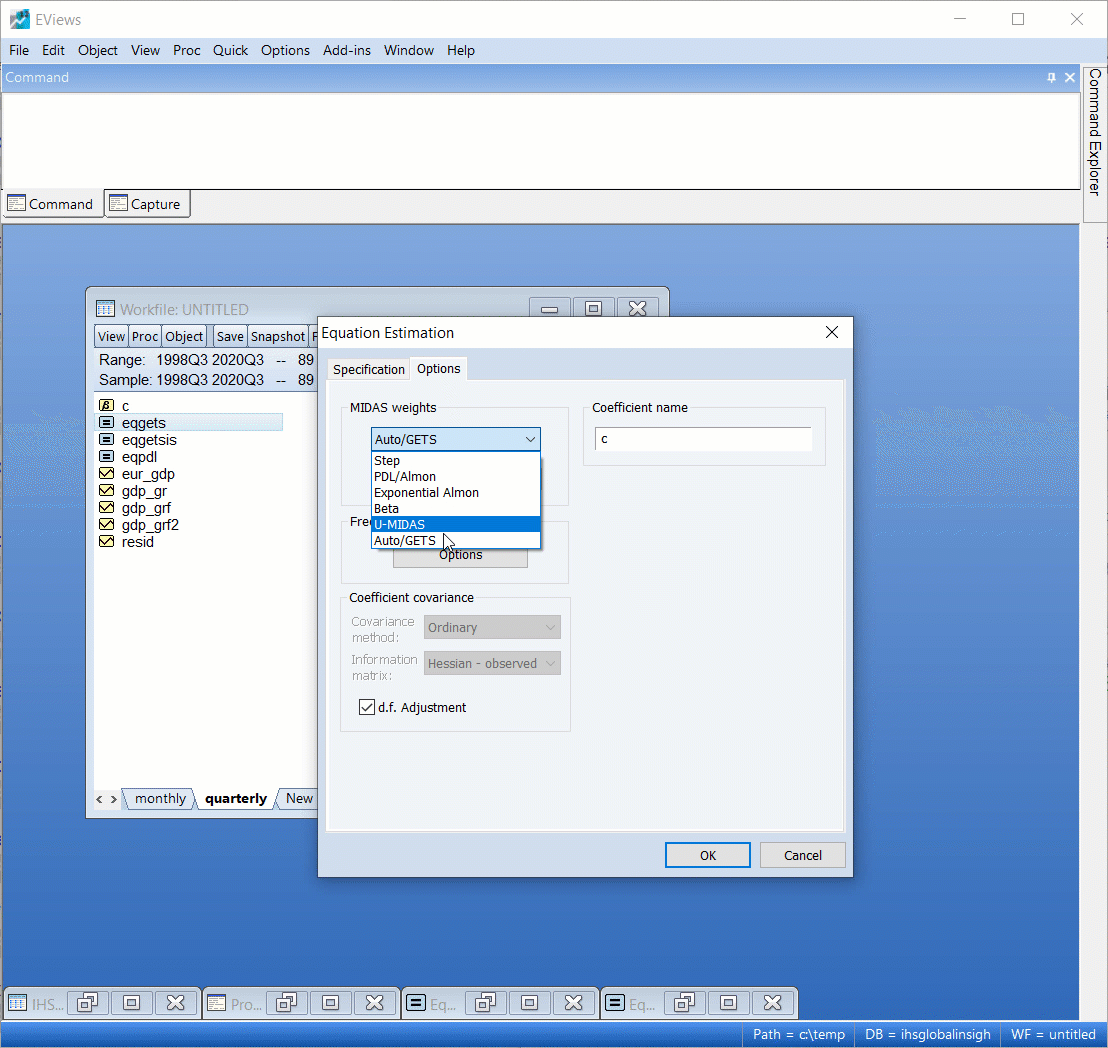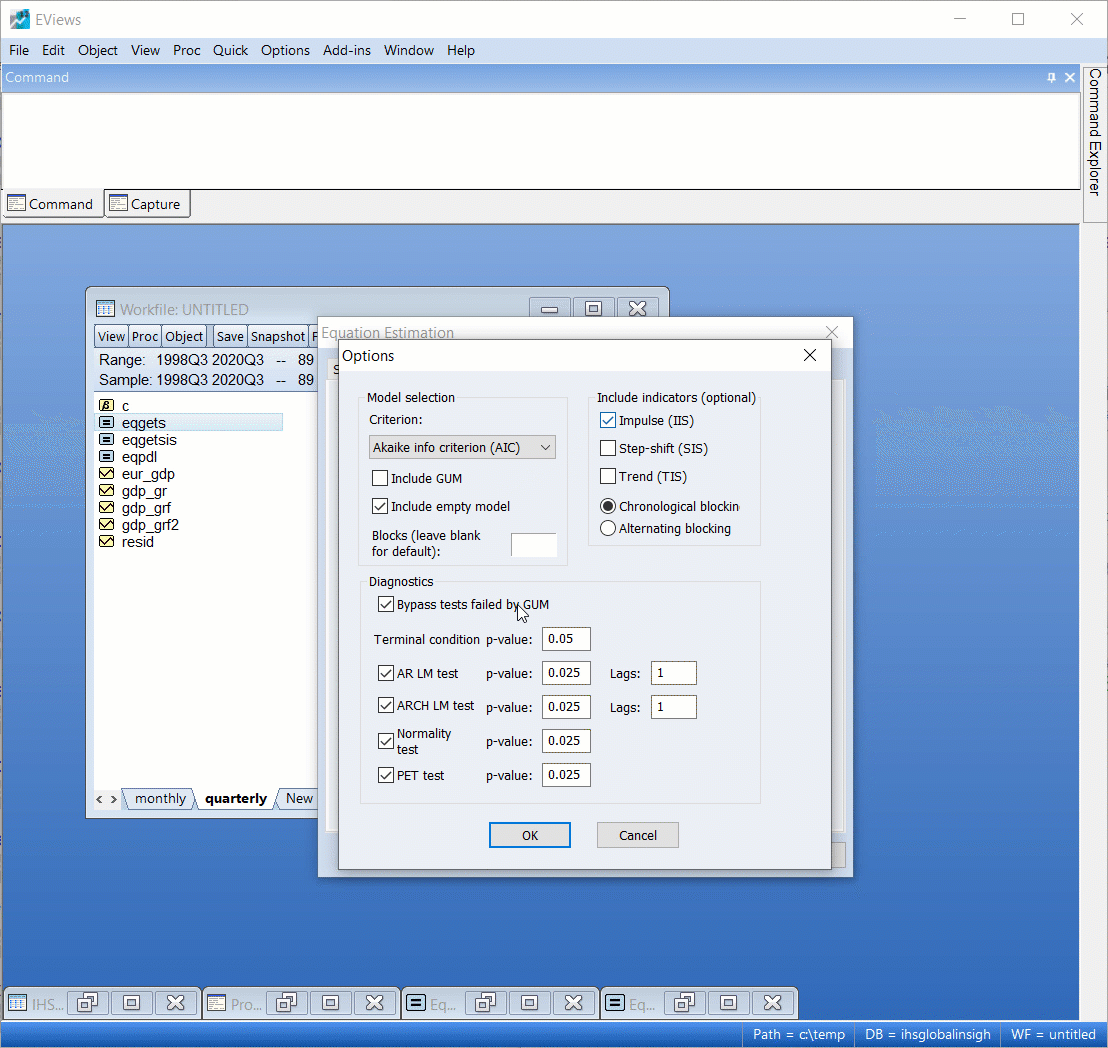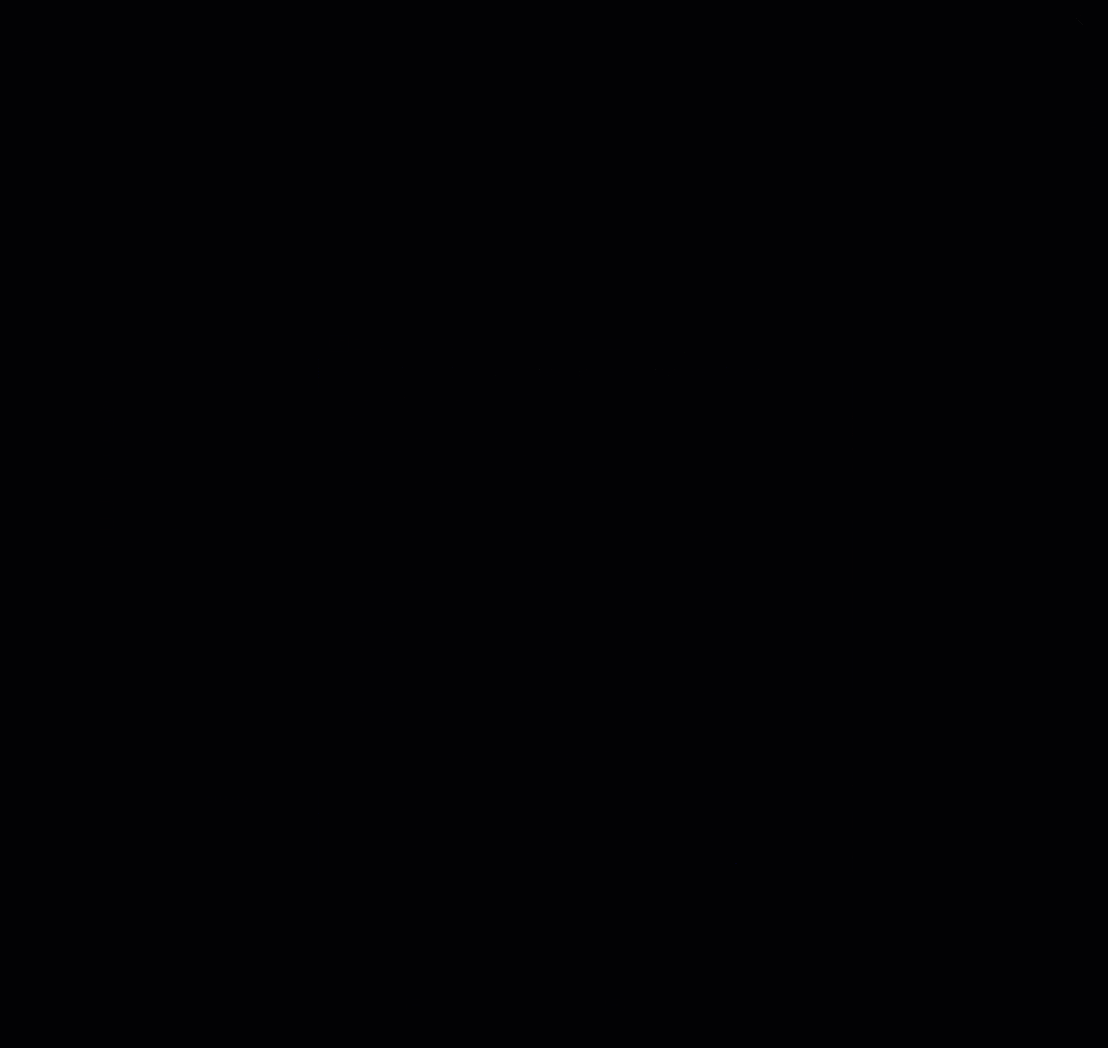 |
 |
The results are worth a quick mention. The GETS routine selected eight periods with outliers. In particular, it included dummy variables for 8 quarters (2001Q1, 2005Q3, 2008Q2, 2008Q3, 2009Q1, 2010Q2, 2011Q2, 2013Q2), and chose to include more months of PMI data: namely, the first and second months of the current quarter, as well as 6, 9 and 12 months prior. In concrete terms, this means, for example, in 2018Q1, the equation chose to use February 2018, January 2018, September 2017, June 2017 and March 2017 as regressors.
Forecasting is performed in the same way, and produces a similar looking forecast to the previous MIDAS-GETS model:
 |
Evaluating Nowcasting Models
The previous examples all performed a single point nowcast of GDP growth and a quick eyeball-test showed that MIDAS-GETS performed well. Here we'll demonstrate a formal nowcast evaluation exercise. In particular, we'll estimate a handful of different models on a rolling basis. The first estimation will again assume we are in February 2018, estimating on data from 1999Q3 through 2017Q4, and will then nowcast 2018Q1. We'll then move a quarter and assume we're in May 2018, estimate through 2018Q1 and nowcast 2018Q2. Next, we'll move another quarter and so on until 2019Q4, meaning we have eight rolling nowcasts.
We'll estimate and nowcast from six different equation specifications:
- A simple AR(1) model with no PMI (GDP growth regressed against a lag and a constant).
- Simple AR(1) model with aggregated PMI (average of the available monthly PMI data).
- PDL/Almon MIDAS with 12 monthly lags of PMI and lagged GDP growth.
- U-MIDAS with 12 monthly lags of PMI and lagged GDP growth.
- MIDAS-GETS with 12 monthly lags of PMI and lagged GDP growth and no indicators.
- MIDAS-GETS with 12 monthly lags of PMI and lagged GDP growth with impulse indicators.
Models 3, 5 and 6 are identical to those we estimated in the early examples. We've written a quick EViews program that will perform these nowcasts:
'create gdp growth series
series gdp_gr = @pca(eur_gdp)
'keep a list of equation names for easier referencing later
%eqlist = "eq_umid eq_agg eq_pdl eq_simple eq_getsis eq_gets"
'create empty forecast series for each equation
group forcs gdp_gr
for %j {%eqlist}
series gdp_{%j}
forcs.add gdp_{%j}
next
'estimate/nowcast loop
for !i=0 to 7
'estimate
smpl @first 2017q4+!i
equation eq_simple.ls gdp_gr c gdp_gr(-1)
equation eq_agg.ls gdp_gr c gdp_gr(-1) agg_pmi
equation eq_pdl.midas(fixedlag=12) gdp_gr c gdp_gr(-1) @ monthly\pmicmpemu(-1)
equation eq_umid.midas(midwgt=umidas, fixedlag=12) gdp_gr c gdp_gr(-1) @ monthly\pmicmpemu(-1)
equation eq_gets.midas(fixedlag=12, midwgt=autogets) gdp_gr c gdp_gr(-1) @ monthly\pmicmpemu(-1)
equation eq_getsis.midas(fixedlag=12, midwgt=autogets, iis) gdp_gr c gdp_gr(-1) @ monthly\pmicmpemu(-1)
'nowcast
smpl 2018q1+!i 2018q1+!i
for %j {%eqlist}
{%j}.forecast temp
gdp_{%j} = temp
d temp
next
next
Once we have the six nowcast series of eight periods each, we can use EViews' built in forecast evaluation engine to compare the nowcasts, by opening up the series containing the true value (GDP_GR) and clicking on View->Forecast Evaluation, and then giving the names of the nowcast series. The results of the is evaluation are:
 |
From the evaluation statistics, we see that the MIDAS-GETS nowcast, GDP_EQ_GETSIS performs very well, with the indicator saturation version giving the lowest RMSE, MAE and SMAPE. The non-indicator version, GDP_EQ_GETS, also performs better than the other traditional MIDAS methods.